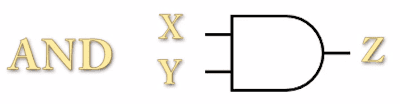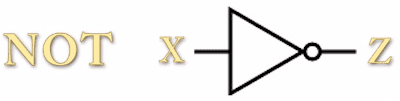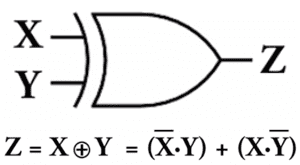Desvendando as Portas Lógicas

Dentre os componentes mais elementares da eletrônica digital estão as denominadas portas lógicas. Elas são integradas aos milhares em circuitos prontinhos para uso, tais como os microprocessadores e os microcontroladores.

O entendimento do funcionamento desses circuitos básicos é essencial para a compreensão dos operadores lógicos usados em programação, principalmente os operadores lógicos bitwise, ou seja aqueles que operam a nível de bit.

Produzi um vídeo com base neste artigo, para um entendimento mais claro das montagens.

Introdução

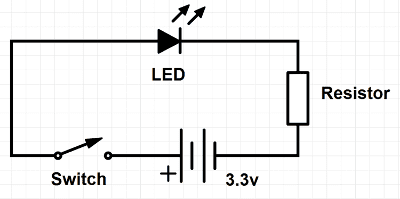
A figura acima apresenta o circuito eletrônico mais elementar que existe: um LED, em série com um resistor limitador de corrente, que acende e apaga ao ser acionada uma chave. Mas embora simples, este circuito contém em si todo o fundamento da eletrônica digital — de fato, o LED só poderá assumir dois estados: apagado, ou aceso; desligado ou ligado; Ø ou 1; falso ou verdadeiro…​ perceberam?

Os transistores funcionam muito bem como chaves eletrônicas e podem comutar, isto é, mudar de estado, com velocidades fantásticas. Com o desenvolvimento da tecnologia, eles puderam ser integrados aos milhões nos microprocessadores, vindo daí a grande capacidade de processamento dos computadores modernos.

Voltando ao nosso conceito básico de eletrônica digital, sabemos então que ela pode representar apenas dois dígitos numéricos: "Ø", para uma tensão de Ø V e "1", para uma tensão de 3,3 V nos circuitos integrados mais modernos, ou 5 V nos mais antigos.

Depois de rever esses conceitos elementares, podemos passar ao estudo das portas lógicas.

Porta "AND"

Esta porta, como diz o nome, faz a operação do "AND" ("E") lógico, que corresponde a uma conjunção, possuindo pelo menos duas entradas. Assim sendo, se "X" e "Y" forem as entradas, a saída "Z" será o resultado da conjunção das entradas (X.Y ou X∧Y). Nas figuras abaixo vemos o símbolo da porta "AND" e sua representação matemática na álgebra booleana.

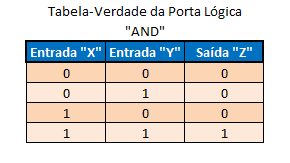
As combinações possíveis decorrentes da aplicação do operador booleano "AND" nas entradas da porta lógica podem ser tabuladas no que é chamado Tabela Verdade. Podemos montar então a Tabela Verdade da porta lógica "AND", conforme a seguir:

Em programação, é mais comum definir a porta lógica "AND" como aquela em que a saída somente será "1" quando todas as entradas forem "1", caso contrário, será "Ø". Se definirmos que "Ø" representa o valor booleano "false" e "1" o valor "true", podemos também definir que o resultado da aplicação de um operador lógico "AND" somente será "true" se ambos os valores comparados forem "true". Caso contrário, o resultado da comparação será "false". Matematicamente, isso é denominado conjunção.

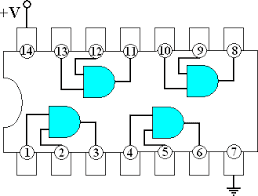
Para a nossa demonstração prática, vamos usar o Circuito Integrado 7408, que contém 4 portas "AND" e cujo diagrama interno é apresentado a seguir.

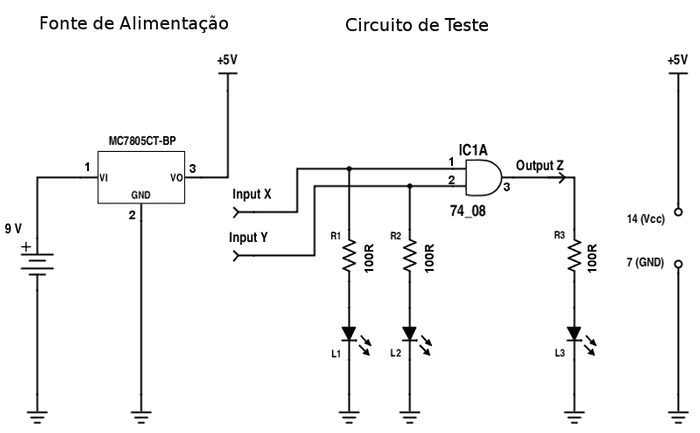
O circuito de teste da porta lógica "AND" é bastante simples, consistindo de dois LEDs em série com as entradas e resistores para limitar a corrente dentro dos seus parâmetros de funcionamento. A alimentação do CI é feita através dos pinos 7 (terra) e 14 (+5Vcc), como consta na extrema direita do esquema e, à esquerda dele, temos uma fonte de alimentação estabilizada usando o CI 7805 e uma bateria de 9V.

A montagem não apresenta nenhuma dificuldade, devendo-se apenas ter cuidado na identificação dos pinos dos CIs e na polaridade dos LEDs. Na foto abaixo, podemos observar que as duas entradas da porta "AND" utilizada (pinos 1 e 2), estão em potencial de ØV, pois os cabos amarelo e azul que os alimentam estão ambos ligados ao terra, confirmado pelos LEDs verdes ligados a elas, que estão apagados. Temos então a primeira situação da Tabela-Verdade da porta lógica "AND" e a saída (pino 3) também apresenta ØV, confirmado pelo LED vermelho ligado a ela, que igualmente permanece apagado.

Passemos agora à verificação da segunda situação da Tabela-Verdade da porta "AND", deixando a entrada "X" aterrada ("Ø" lógico), e ligando o cabo amarelo da entrada "Y" (pino 1) à linha de alimentação positiva de +5V ("1" lógico). Como apenas uma das entradas é "1", a saída continua "Ø", confirmado pelo LED vermelho apagado. Confira na próxima foto:

Passemos à terceira situação possível da Tabela-Verdade da porta "AND", ligando agora o cabo azul da entrada "X" (pino 2) à alimentação de +5V ("1" lógico), voltando a aterrar o cabo amarelo da entrada "Y" (pino 1). Embora invertida, esta situação é idêntica à anterior, ou seja, apenas uma das entradas é "1" e, portanto, a saída ainda permanece "Ø", confirmado pelo LED vermelho apagado. Esta situação está demonstrada no foto a seguir:

A última situação possível na Tabela-Verdade da porta lógica "AND" é aquela em que ambas as entradas estão ligadas à linha de alimentação de +5V, no estado de "1" lógico, conforme pode ser constatado por ambos os LEDs verdes acesos. Esta é a única situação em que a saída também apresenta "1" lógico, confirmado pelo LED vermelho aceso. Veja a foto:

Para melhor comparar o resultado visual das entradas e saída nas fotos com a situação da Tabela-Verdade da porta lógica "AND", tenha sempre em mente que:

• LED apagado = "Ø"
• LED aceso = "1"

Porta "OR"

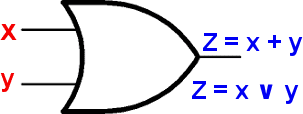
A porta lógica "OR" faz a operação do "OR" ("OU") lógico, que corresponde a uma disjunção, possuindo também pelo menos duas entradas, tal como na porta "AND". Dessa forma, se "X" e "Y" forem as entradas, a saída "Z" será o resultado da disjunção das entradas (X+Y ou X∨Y).

Na figura abaixo vemos o símbolo da porta "OR" e sua fórmula matemática em álgebra booleana na saída (Z).

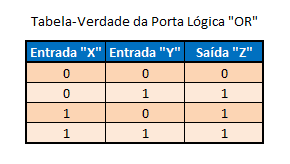
A tabela-verdade da porta lógica "OR" é apresentada a seguir:

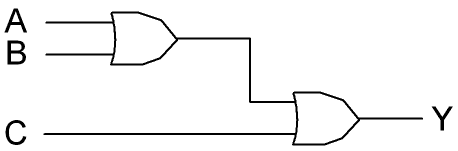
Na tabela acima podemos observar que a saída da porta lógica "OR" somente será "Ø" se todas as suas entradas forem "Ø", caso contrário, será "1". Tanto na porta "AND", como agora na porta "OR", afirmamos que elas possuem pelo menos duas entradas, mas estas podem ser expandidas, se for necessário, acoplando-se outra porta "OR" a uma das entradas, como representado esquematicamente na figura abaixo.

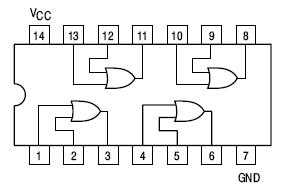
Para a demonstração prática desta porta lógica, vamos usar outro circuito integrado TTL, o 7432, cujo diagrama é mostrado na próxima figura, na qual podemos ver que ele contém 4 portas "OR" no seu interior. A alimentação é provida através dos pinos 7 (terra) e 14 (+5Vcc), como nos demais integrados que estamos usando.

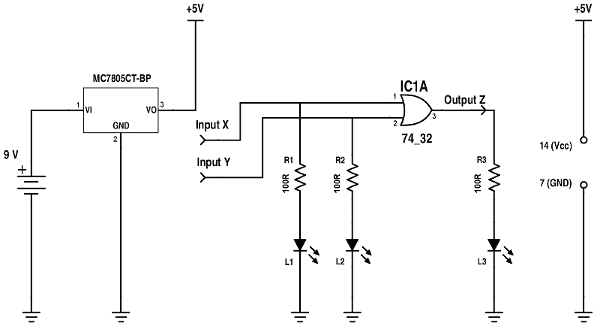
Para quem fez a montagem anterior da porta lógica "AND", agora é uma barbada. Basta substituir o 7408 pelo 7432 e aproveitar todas as demais ligações da protoboard. Na figura abaixo, temos o esquema do circuito da porta lógica "OR" que, como se vê, é similar ao da porta "AND", exceto quanto ao Circuito Integrado utilizado. O valor dos resistores pode se situar tranquilamente entre 100Ω e 150Ω para assegurar um brilho adequado dos LED, dentro dos limites de segurança.

Porta "NOT" (Inversora)

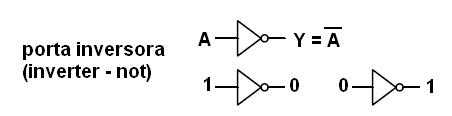
A lógica desta porta é simplíssima: como o nome já diz, ela faz uma inversão da entrada. Ou seja, quando a tensão na entrada é nula (0 V), que podemos representar por 0, a tensão na saída será alta (3,3 V, por exemplo), e podemos representá-la por 1. Por outro lado, se a entrada for alta (3,3 V neste exemplo), a saída será nula (0 V). Abaixo podemos ver o símbolo da porta inversora e a representação da lógica do seu funcionamento.

Aquele pequeno círculo na frente do triângulo quer dizer inversão. Voltaremos a ver isso quando examinarmos as outras portas lógicas.

Podemos montar uma simples porta inversora, usando apenas um transistor NPN, alguns resistores, uma chave "push-button" e dois LEDs de cores diferentes, para monitorar a entrada e a saída.

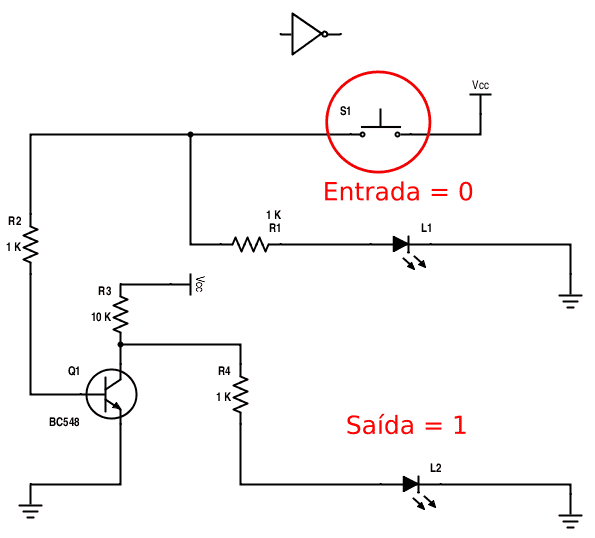
O circuito, apresentado na figura abaixo, é bem simples e sua montagem pode ser feita numa protoboard, usando alguns cabinhos para as conexões.

Nesta situação, com o push-button aberto, o LED de entrada recebe uma tensão desprezível, praticamente Ø V, e permanece apagado (representando Ø); por outro lado, a polarização do transistor permite fluir uma corrente suficiente pelo coletor para acender o LED de saída, com uma tensão praticamente nominal (representando 1). A foto a seguir mostra a montagem neste estado.

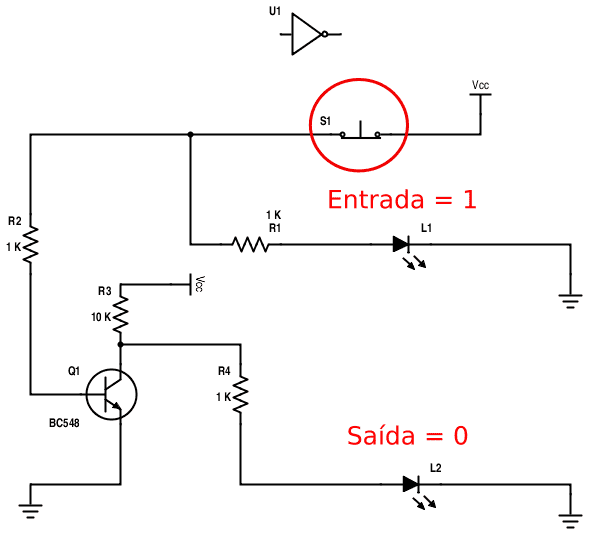
Vamos inverter as coisas agora, conforme mostrado no diagrama abaixo:

Quando pressionamos o botão, a corrente flui livremente pelo LED de entrada que acende com a tensão nominal (representando 1), alterando-se a polarização do transistor que entra em corte e, uma vez que a corrente de coletor praticamente inexiste, o LED de saída permanece apagado (representando Ø). A próxima foto exibe a montagem neste novo estado.

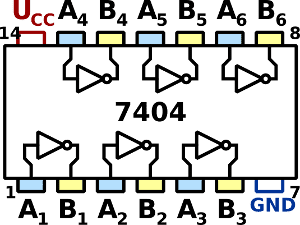
Como já disse, esses circuitos são embutidos em circuitos integrados, como o famoso 7404, já um ancião, que possui nada mais nada menos do que seis portas inversoras, operando com uma tensão nominal de 5 V e cujo diagrama interno é exibido na figura seguinte.

Este CI faz parte da família TTL (sigla para Transistor-Transistor Logic ou Lógica Transistor-Transistor em português), que já teve seu momento na história da eletrônica. Os TTL tem a vantagem de não serem tão sensíveis à eletricidade estática como os da família CMOS mais moderna, e são de baixo custo, razões suficientes para usá-los nas nossas experimentações com as portas lógicas.

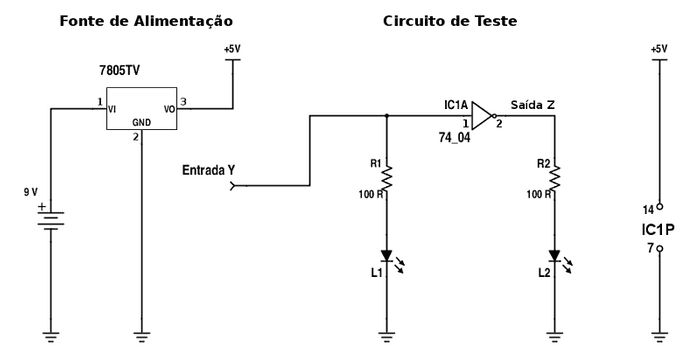
Apresento abaixo o circuito para teste de uma porta inversora (NOT), usando o 7404, que simplifica bastante a montagem. Para esta demonstração, vamos usar apenas uma das portas inversoras disponíveis, correspondendo aos pinos 1 (entrada) e 2 (saída) do CI. O pino 7 corresponde sempre ao terra e o pino 14 à alimentação de 5 Vcc, conforme se vê na extrema direita do diagrama. A tensão de alimentação é crítica e, caso você não possua uma boa fonte ajustável regulada, apresento à esquerda o esquema para uma fonte estabilizada usando o CI 7805TV (ou equivalente), garantindo uma saída de 5V, a partir de uma bateria de 9V.

Na foto abaixo, vemos a montagem do circuito com a entrada aterrada (cabo amarelo), ou seja, "Ø", cuja condição é atestada pelo LED indicador verde apagado, enquanto a saída apresenta a tensão nominal de 5V, isto é, "1", conforme confirma o seu LED indicador vermelho aceso.

Observe na foto seguinte que invertemos a polarização da entrada (cabo amarelo), alimentado agora com a tensão nominal de 5V, ou seja, "1", de forma que seu LED indicador acende, enquanto a saída é aterrada, isto é, "Ø", apagando-se o LED indicador vermelho.

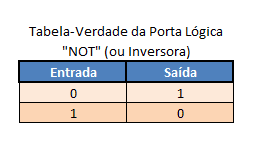
Fica confirmada experimentalmente, portanto, a tabela-verdade da porta lógica "NOT" (ou inversora), qual seja:

Para encerrar o estudo desta porta, apresento na figura abaixo o símbolo para a porta lógica "NOT", onde o terminal X corresponde à entrada e o terminal Z à saída.

A representação matemática na álgebra booleana para esta porta é a apresentada na figura seguinte. A linha acima da letra "Y" indica o inverso de "Z".

Porta "XOR"

Esta porta apresenta na sua saída o resultado de operações booleanas com as três portas vistas anteriormente, que são as básicas. Apresento a seguir o operador da porta "XOR" e seu símbolo lógico nos diagramas dos circuitos eletrônicos:

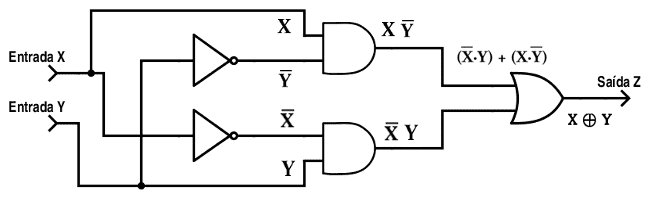
Como podem observar, a operação "XOR" pode ser decomposta numa operação "OR" do resultado de uma operação "AND" entre o inverso da entrada "X" com a entrada "Y" e outra operação "AND" entre a entrada "X" e o inverso da entrada "Y". Dessa forma, é possível montar um circuito lógico da porta "XOR", usando as portas básicas, conforme o diagrama a seguir:

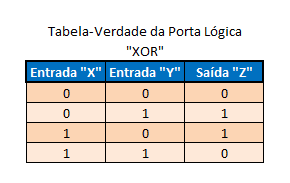
A tabela verdade da porta lógica "XOR" é a seguinte:

Vemos que somente teremos o "1" lógico na saída da porta "XOR" quando os valores lógicos das entradas forem diferentes, isto é, "Ø" e "1" ou "1" e "Ø". Quando os valores lógicos das entradas forem iguais ("Ø" e "Ø" ou "1" e "1"), a saída será "Ø" lógico. Daí vem o nome da porta, que é uma abreviatura para "eXclusive OR" ("OU exclusivo").

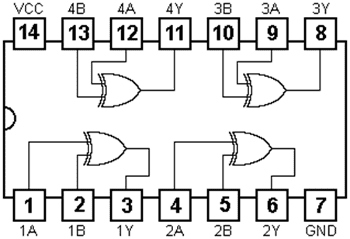
Para teste da porta lógica "XOR" usaremos um circuito integrado 74_86, que abriga 4 portas lógicas "XOR" no seu interior. No diagrama a seguir, podemos identificar a pinagem deste CI:

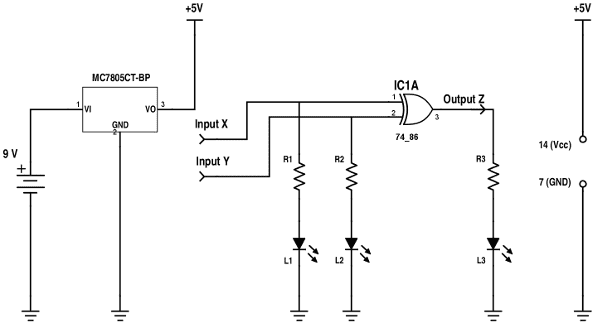
O circuito de teste é praticamente idêntico ao das portas "AND" e "OR", bastando substituir o circuito integrado na protoboard, respeitando a posição dos pinos. A seguir, o diagrama do circuito:

Conclusão

Espero que este artigo e o vídeo que o complementa tenham esclarecido para vocês os fundamentos da álgebra booleana e sua aplicação nos circuitos eletrônicos que, por sua vez, são a base dos operadores lógicos utilizados nas linguagens de programação. Evidentemente, num pequeno artigo como este, abordamos apenas os fundamentos básicos da matéria, mas espero ter despertado seu interesse para aprofundar-se nos estudos da álgebra boolena e na montagem de circuitos práticos de maior complexidade. O assunto é fascinante e, com certeza, seu entendimento é essencial para dominar a lógica de programação.